前言:就我個人而言,部分分式的技巧在做裂項求數列總和,有理函式的積分時都常常用到,但是方法不勝枚舉,故作此整理,以便查閱溫習。
簡介:部分分式(Partial fraction decomposition),是將有理函數分解成許多次數較低有理函數和的形式,來降低分子或分母多項式的次數。分解後的分式需滿足以下條件:
- 分式的分母需為不可約多項式(irreducible polynomial)或其乘冪。
- 分式的分子多項式次數需比其分母多項式次數要低。
註:以上內容摘自維基百科,詳閱此處。
我目前總共整理了四種較為常用的Method,而其各有適合應對的場合,將來若有學到新的方法會陸續在此補上(實際上是更高階的方法我目前還沒辦法理解,有機會會嘗試去學看看)。
----------------------------------------------------------------------------------------------
我目前總共整理了四種較為常用的Method,而其各有適合應對的場合,將來若有學到新的方法會陸續在此補上(實際上是更高階的方法我目前還沒辦法理解,有機會會嘗試去學看看)。
- 比較係數法
- 一手遮天法
- 留數法
- 借複生子法
----------------------------------------------------------------------------------------------
比較係數法
我個人認為此法計算過程時間過於冗長,但是這是最萬用的Method,若是透過一手遮天或留數法都沒有辦法順利求出分式時,此法才會用使用的機會。總體來說,是最基本的方法,但在我們學會其他方法後,能不用就不用,避免浪費時間。
展開等號右邊的式子得:
等號兩邊進行比較,進而有:
原式前半部分則可寫為:
積分後得:
接下來處理原式後半部分,換元後有:
故原式為:
一手遮天法
此法是最常用的,求分式的速度極快,應掌握嫻熟,但其仍有不適合使用的時機,例如分母有高次項的因式出現時。
我們先給定一等式:
(x-b)(x-c)}=\frac{A}{x-a}+\frac{B}{x-b}+\frac{C}{x-c})
假設我們要先求A的值,就將等號兩邊同乘以其對應項的分母:(x-c)}=A+\frac{B}{x-b}(x-a)+\frac{C}{x-c}(x-a))
從而,當x=a時,等號右邊的第二項及第三項為0,進而:
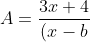(x-c)}\mid&space;_{x=a})
B、C亦同理。
----------------------------------------------------------------------------------------------
之後同乘左邊等式分母有最高幂次的因式,得(a):
}{s(x)}=A(x-a)^{2}+B(x-a)+C+r(x)(x-a)^{3})
其中C等於(通常第一次的留數法使用改用一手遮天會較快):
}{s(x)}=A*0+B*0+C+r(x)*0)
而後微分(a)一次,得:
![\frac{d}{dx}(\frac{p(x)}{s(x)})=2A(x-a)+B+0+[r(x)(x-a)^{3}+3r(x)(x-a)^{2}]](https://latex.codecogs.com/gif.latex?\frac{d}{dx}(\frac{p(x)}{s(x)})=2A(x-a)+B+0+[r(x)(x-a)^{3}+3r(x)(x-a)^{2}])
其中B等於:
}{s(x)}))
重覆上二步驟,同理可得A:
}{s(x)}))
我們先給定一等式:
)}=\frac{Ax+B}{[(x-a)^{2}+b^{2}]}+r(x)](https://latex.codecogs.com/gif.latex?\frac{p(x)}{[(x-a)^{2}+b^{2}](s(x))}=\frac{Ax+B}{[(x-a)^{2}+b^{2}]}+r(x))
Example:(x^{2}+1)}=\frac{Ax+B}{x^{2}+4x+5}+\frac{Cx+D}{x^{2}+1})
求A、B,將兩邊同乘其對應項的分母,從而有:}={Ax+B}+r(x)(x^{2}+4x+5))
我們令其剛剛乘掉的分母等於零,再透過公式解可得 ,之後取正的帶入上式,
,之後取正的帶入上式,
再進行約分整理後得:
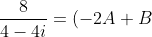+Ai)
進一步化簡後(上式用了平方差公式來化簡),可得A=1;B=3
C、D的求法亦同理。
假設我們要先求A的值,就將等號兩邊同乘以其對應項的分母:
從而,當x=a時,等號右邊的第二項及第三項為0,進而:
B、C亦同理。
----------------------------------------------------------------------------------------------
留數法
此法可視為處理一手遮天法的弊病的方法。
之後同乘左邊等式分母有最高幂次的因式,得(a):
其中C等於(通常第一次的留數法使用改用一手遮天會較快):
而後微分(a)一次,得:
其中B等於:
重覆上二步驟,同理可得A:
----------------------------------------------------------------------------------------------
借複生子法
此處理方法跟一手遮天大同小異,但特別的是「此法在最後會進行實部與虛部的比較」,而使用一手遮天法時若要求x為複數時,到最後比較的過程往往直接將複數代回x就可以得到等號兩邊都為實數的形式,而借複生子法則往往無法通過代回x的步驟,直接進行求解。我們先給定一等式:
Example:
求A、B,將兩邊同乘其對應項的分母,從而有:
我們令其剛剛乘掉的分母等於零,再透過公式解可得
再進行約分整理後得:
進一步化簡後(上式用了平方差公式來化簡),可得A=1;B=3
C、D的求法亦同理。
----------------------------------------------------------------------------------------------
請問CX+D項怎麼不見的?
回覆刪除上述問題是針對"借複生子法"中(Example:題目中,求A、B,將兩邊同乘其對應項的分母)這一步驟,請問CX+D項如何消除?
回覆刪除同乘上(x^2+4x+5)之後帶入x=-2+-i 就會變成0了
刪除